Basic Antenna Parameters

These are some terms that antenna engineers use to describe an antenna and it’s performance. Knowing some of these terms allow us to speak the same language when selecting an antenna and characterizing its performance!

📄 Posted: 2021-11-02 11:35:54 ✔️ Updated: 2024-02-05 09:25:09

Summary of Important Antenna Parameters

Below are quick links to the antenna performance terms explained in this article.

Antenna Term	Quick Definition
Axial Ratio	Polarization deviation from pure orthogonal components
Efficiency	Ratio of energy radiated and energy supplied
EIRP / Gain	Typically, maximum energy radiated around an antenna
Fractional Bandwidth	Frequency bandwidth in percent
Front to Back Ratio	Divide boresight gain over the reverse gain
Half Power Beam Width	Angle between the half-power points of the main lobe
Pattern	Radiation in a sphere all around the antenna
Polarization	Direction at which the electrical energy oscillates
Quality Factor	Antenna bandwidth relative to center frequency
Return Loss / VSWR	Ratio of energy thru and returned back to the input port

What is an Antenna?

An antenna is defined as a metallic structure that can radiate or receive radio frequency signals.

What is Antenna EIRP / Gain?

The EIRP or Effective Isotropic Radiated Power is the amount of energy spread around an antenna. This varies based on antenna architecture and if a single value is given, it’s typically the maximum. Most of the time, units are given in dBm, but they also could be given in dBc (power related to the carrier) or dBd (power related to an ideal dipole). It’s computed by combining the gain of the amplifier stage with the gain of the antenna as shown in the formula below.

Gain of an antenna is only the energy that is possible to radiate including feed losses. The higher the number, the more power can be radiated in that direction.

There is a trade-off between antenna gain, and the so called half power beam width (see below) of the antenna: The larger the gain value, the more narrow the antenna main beam will be.

Given the input power from a transmitter radio, Pt (dBm), the losses, L (dB), and the Gain of the antenna, G (dBi), the EIRP (dBm) can be calculated as follows.

(1) $\begin{equation*} EIRP = P_t - L + G \end{equation*}$

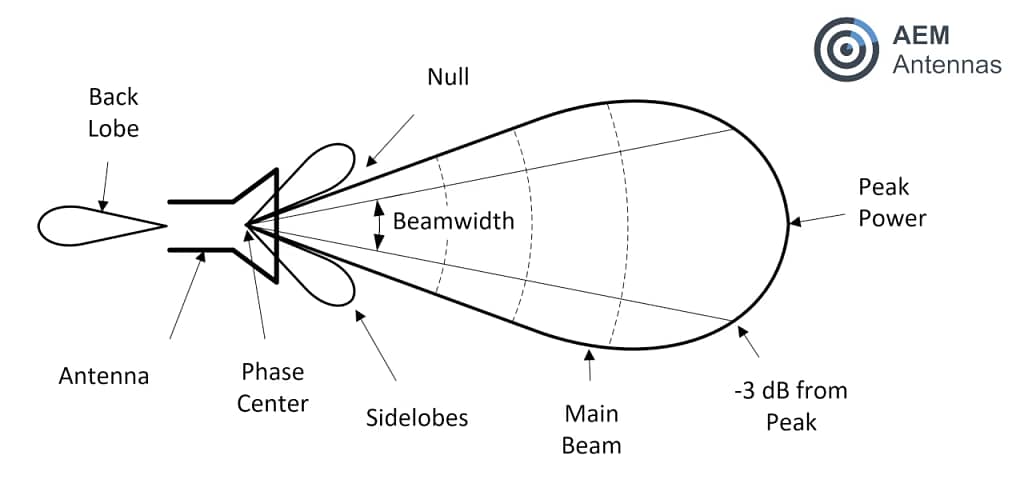
What are Antenna Patterns?

An antenna pattern is a measure of the radiation in a sphere all around the antenna. Typically, antenna radiation patterns are given as E-plane or H-plane cuts of the sphere. The E-plane pattern contains the maximum electric field vector and the H-plane contains the maximum magnetic field vector.

Field patterns can be described as omni-directional, radiating in all directions, or directional, with a focused main beam in a certain direction.

Half Power Beam Width (HPBW)

If an antenna is described to be directional with a main lobe, it is characterized mainly by gain. The HPBW is the angle between the half-power points of the main lobe from the peak gain of the main lobe (ie: angle between max gain and next gain -3dB down). Both of this parameters can give an idea of the expected radiation pattern.

An Antenna Return Loss / VSWR

An antenna return loss is given by the amount of energy returned back to the input port and is an important antenna performance term.

To radiate a radio’s power into free space, the radio must be matched to the antenna (and the antenna matched to free space!). Any energy not transmitted or absorbed as loss is reflected back to the radio. Measuring this reflected power is called Return Loss or the Voltage Standing Wave Ratio.

A typical PCB microstrip is match to a 50ohm characteristic impedance. In reality, an antenna will not be exactly matched producing a mismatch coefficient, Gamma. Gamma is the linear term and Return loss is given in units of dB. The Return Loss can be calculated from the antenna input impedance as follows.

(2) $\begin{equation*} \Gamma = \frac{Z_{in} - Z_c}{Z_{in} + Z_c} \end{equation*}$

(3) $\begin{equation*} RL = 20\log10(\|\Gamma\|) \end{equation*}$

System designers will want to target small VSWR values where a minimum value is given by 1. Typical VSWR values are between 1 and 2. Return Loss is given in units of dB and typical values would be less than -10dB at center frequency.

We can compute VSWR from measured Return loss by the following.

(4) $\begin{equation*} \Gamma = 10^{RL/20} \end{equation*}$

(5) $\begin{equation*} VSWR = \frac{1+\|\Gamma\|}{1-\|\Gamma\|} \end{equation*}$

The following is a Return Loss to VSWR conversion table.

RL	VSWR	RL	VSWR	RL	VSWR
-1	17.4	-11	1.8	-21	1.20
-2	8.7	-12	1.7	-22	1.19
-3	5.8	-13	1.6	-23	1.15
-4	4.4	-14	1.5	-24	1.13
-5	3.6	-15	1.43	-25	1.12
-6	3.0	-16	1.38	-26	1.11
-7	2.6	-17	1.33	-27	1.09
-8	2.3	-18	1.29	-28	1.08
-9	2.1	-19	1.25	-29	1.07
-10	1.9	-20	1.22	-30	1.065

Return Loss / VSWR Conversion Table

Antenna Efficiency

The overall antenna efficiency is computed by taking into account all losses of the antenna right up to the aperture. Simply put, it is the ratio of energy radiated over the energy supplied at the input port.

(6) $\begin{equation*} e_{tot} = \frac{{P}_{rad}}{{P}_{in}} \end{equation*}$

Losses can include reflections due to transmission line mismatches, conductor, and dielectric losses. The total efficiency factor can be found by measuring dielectric and conduction efficiency (or by using a calibrated simulator) and by knowing the reflection coefficient.

(7) $\begin{equation*} e_{factor} = {e}_{cond}e_{diel}(1-\|\Gamma_{r}\|^2) \end{equation*}$

Antenna Quality Factor

The Q or Quality Factor of an antenna is computed from the bandwidth relative to center frequency.

So called ‘High-Q Antennas’ are very narrow band and have a deep resonance. At center frequency, they have a very high efficiency. ‘Low-Q Antennas’ have wide bandwidths but are known to have high loss.

If the loss of the antenna is known along with the Return Loss, Q can be calculated by the following.

(8) $\begin{equation*} \Gamma_{rl} = 10^{RL/20} \end{equation*}$

(9) $\begin{equation*} \Gamma_{il} = 10^{IL/20} \end{equation*}$

(10) $\begin{equation*} Q = \Gamma_{rl}^2 + \Gamma_{il}^2 \end{equation*}$

Knowing the band edges given by f1 and f2, the antenna Q can be also calculated as follows.

(11) $\begin{equation*} Q = \frac{(f_2 + f_1)}{2(f_2 - f_1)} \end{equation*}$

The Fractional Bandwidth

Similar to the Q-factor, the Fractional Bandwidth (FBW) is a measure of the antenna frequency bandwidth in percent where typical antennas are between 10-20%, and Ultra Wideband (UWB) antennas are >50%.

(12) $\begin{equation*} FBW = \frac{1}{Q} = \frac{2(f_2 - f_1)}{(f_2+f_1)} \end{equation*}$

Gain Front to Back Ratio

An antenna Front to Back ratio is computed by dividing the boresight gain (direction of maximum gain) with the reverse gain (typically minimum gain in the opposite direction of boresight) given in dB.

(13) $\begin{equation*} FBW = 10\log10( \frac{G_{fwd}}{G_{back}} ) \end{equation*}$

Antenna Polarization

The antenna polarization is defined as the direction at which the electrical energy oscillates. An antenna polarization can be classified as Linear, Circular, or Elliptical.

If the electric field vector is always along one axis (ie: x- or y-axis, with propagation along z), it is said to be linearly polarized (ie: horizonal or vertical).

If the electric field vector traces a circle, it is said that it is circularly polarized (ie: Left Hand Circularly Polarized or Right Hand Circularly Polarized).

Circular Polarized Axial Ratio

For circularly polarized antennas, the Axial Ratio (AR) is an important parameter. It indicates the deviation from pure orthogonal E-field components forming the circular polarization.

Typically, a target of 0dB is desired for center frequency and less than 2dB over the band.

Feed axial ratio can be calculated from the s-parameters as follows given the common port (horn interface) by the following.

Given the common port (com) is square or circular with two linear ports (VP, HP) associated to compute the port s-parameters, and P1 and P2 are the 2 circularly polarized ports of the system:

(14) $\begin{equation*} IL_{LHCP} = \frac{S_{com:VP}+jS_{com:HP}}{\sqrt2} \end{equation*}$

(15) $\begin{equation*} IL_{RHCP} = \frac{S_{com:VP}-jS_{com:HP}}{\sqrt2} \end{equation*}$

(16) $\begin{equation*} a = \|IL_{RHCP}\| + \|IL_{LHCP}\| \end{equation*}$

(17) $\begin{equation*} b = \|(\|IL_{RHCP}\| - \|IL_{LHCP}\|)\| \end{equation*}$

(18) $\begin{equation*} AR_{dB} = 20\log10( \frac{a}{b} ) \end{equation*}$

We hope this post helped you get around some common antenna performance terms.

Let us know how we did by getting in contact with us!

If you liked this article, then please share it on LinkedIn.

Learn More About Us In Our Latest Articles & Press Releases

When to Involve An Antenna ConsultantOctober 23, 2022
Professional Antenna Design SoftwareMay 9, 2022
Selecting the Best Antenna for a Wireless SystemMarch 20, 2022
AEM Antennas joins the Ansys Startup ProgramJanuary 29, 2022
Our Customers and Vendors are at the Forefront of Everything We DoJanuary 23, 2022
Basic Antenna ParametersNovember 2, 2021
Antenna Design ToolsOctober 16, 2021
A Practical Guide for Antenna Matching CircuitsAugust 2, 2021

View All Articles